暗号技術における安全性(公開鍵暗号方式)
はじめに
ブロックチェーンスタジオでは、データセットから個人を特定することを防ぐ技術に関する研究を行っており、その一環で暗号技術に関する勉強を行っています。今回は、その中で公開鍵暗号方式の安全性に関する知識として、下記について紹介したいと思います。
- 公開鍵暗号方式の説明
- 公開鍵暗号方式の暗号文を解読する難易度
- 公開鍵暗号方式の安全性の解説
なお、公開鍵暗号方式については、共通鍵暗号方式と共通的な知識が多いためこの記事も読んでいただけるとありがたいです。
公開鍵暗号方式
概要
共通鍵暗号方式とは、以前の記事で紹介した通り、データの送信者と受信者の間で別々の鍵を使用し、データの暗号や復号を行う方式です。
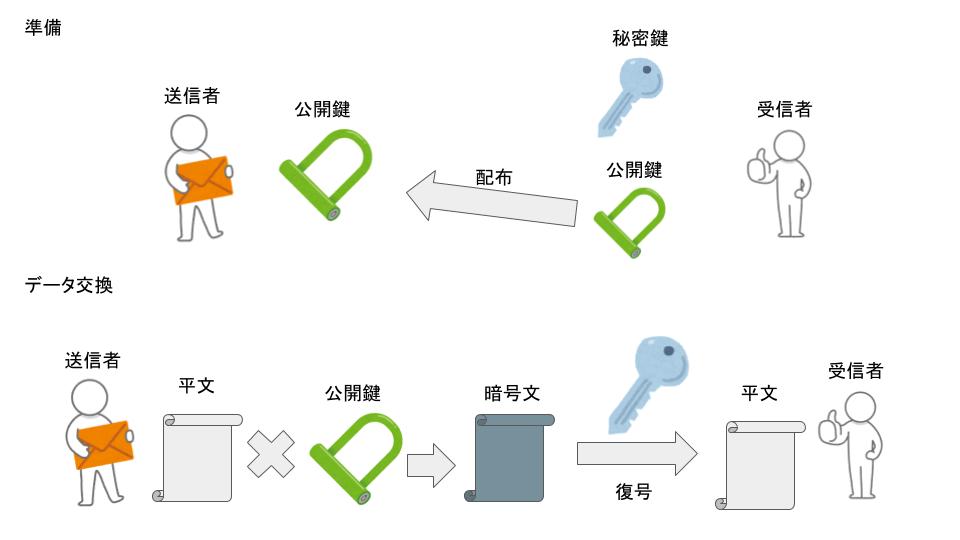
共通鍵暗号方式との比較
公開鍵暗号方式は、秘密鍵と公開鍵の2つを用意できるため、共通鍵暗号方式と比較すると下記のような利便性があります。
- 鍵配送の容易さ
共通鍵暗号方式では、暗号通信の当事者が鍵を秘密裏に共有する必要があります。
一方で、公開鍵暗号方式は、暗号化と復号化で異なる鍵を利用するため、秘密裏に鍵を共有する必要がない分、鍵配送が容易になります。
ただし、通信路が公開されていると、攻撃者に偽の鍵を渡されて傍受される危険性がある(中間者攻撃)ため、相手の公開鍵であるという正当性を確認する仕組みを構築する必要があります。 - 所有鍵数の減少
n人の利用者が互いに暗号通信を行うことを想定します。
この際、共通鍵暗号方式では、通信相手に応じて鍵を生成する必要があるため、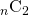 個の鍵が必要となります。
個の鍵が必要となります。
一方で、公開鍵暗号方式では、送信者と受信者が、互いに公開鍵を交換するだけで済むため、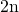 個の鍵ペアを生成するだけで済むという利便性があります。
個の鍵ペアを生成するだけで済むという利便性があります。
公開鍵暗号方式の解読
暗号文の強度
公開鍵暗号方式は、暗号化と復号化に利用する鍵が異なります。数式で表した場合、平文 ![]() , 秘密鍵
, 秘密鍵 ![]() , 公開鍵
, 公開鍵 ![]() , 暗号化関数 $Enc$, 復号化関数
, 暗号化関数 $Enc$, 復号化関数 ![]() としたとき、下記のようになります。
としたとき、下記のようになります。
![]()
このため、暗号文 ![]() から秘密鍵
から秘密鍵 ![]() を推測されないことが、暗号文の強度の指標となります。公開鍵暗号方式では、これらは下記のように分類されています。
を推測されないことが、暗号文の強度の指標となります。公開鍵暗号方式では、これらは下記のように分類されています。
- 秘匿性:
暗号文の部分情報について得られるかという指標です。下記の2段階に設定されています。- 一方向性(OW: One Wayness):
暗号文 から平文
から平文 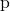 が得られないこと。具体的には、暗号化の関数
が得られないこと。具体的には、暗号化の関数 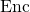 (もしくは、公開鍵
(もしくは、公開鍵 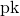 )と暗号文
)と暗号文  を用いて平文
を用いて平文 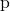 を得ることができないこと。
を得ることができないこと。 - 強秘匿性(IND: Indistinguishability):
OWに加えて、暗号文 から平文
から平文 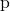 のいかなる部分情報も得られないこと。具体的には、「平文が
のいかなる部分情報も得られないこと。具体的には、「平文が 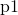 、
、 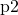 の組み合わせであり、暗号化の関数
の組み合わせであり、暗号化の関数 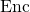 (もしくは暗号化に必要となる鍵
(もしくは暗号化に必要となる鍵 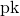 )を攻撃者が知っているという前提がある。この上で暗号文
)を攻撃者が知っているという前提がある。この上で暗号文  を与えられたとしても攻撃者が暗号文
を与えられたとしても攻撃者が暗号文  から平文が
から平文が 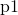 なのか
なのか 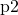 なのかを求めることができない(もしくは困難である)」といった状況が成り立つような秘匿性を確保していること。
なのかを求めることができない(もしくは困難である)」といった状況が成り立つような秘匿性を確保していること。
- 一方向性(OW: One Wayness):
- 頑強性(NM: Non Malleability):
ある平文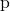 から暗号文
から暗号文  を生成する関数
を生成する関数 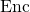 (
( 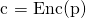 )を知っていることを前提とする。この際、平文
)を知っていることを前提とする。この際、平文 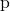 と
と 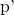 の暗号文
の暗号文  と
と 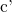 を知った際に、
を知った際に、  と
と 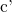 から平文
から平文 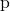 と
と 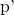 の関係を推測することができないこと。(例えば、平文の関係性が
の関係を推測することができないこと。(例えば、平文の関係性が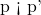 の際に、暗号文も
の際に、暗号文も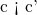 であるという関係性が成り立つことが分からないこと)
であるという関係性が成り立つことが分からないこと)
また、セキュリティの強度としては、「 ![]() 」の順で安全性が高いことが証明されています。
」の順で安全性が高いことが証明されています。
攻撃手法の強弱について
公開鍵暗号方式と共通鍵暗号方式は、同じ攻撃手法を用いることができます。
しかし、公開鍵暗号方式の場合、暗号オラクルを得ることは簡単だが、復号オラクルを得ることができる状況は限定されています。
このため、攻撃手法の強弱としては、「 ![]() 」の順になります。
」の順になります。
解読難易度の指標
公開鍵暗号方式では、安全性と攻撃方法の組み合わせの中で、どの要件を満たせるのかを指標として暗号化アルゴリズムの安全性指標が証明されています。
具体的には、下記のような関係性(矢印方向に安全性が高い)が証明されています。
| OW | IND | NW | |||
|---|---|---|---|---|---|
| CPA | OW-CPA | → | IND-CPA | → | NW-CPA |
| ↓ | ↓ | ↓ | |||
| CCA1 | OW-CCA1 | → | IND-CCA1 | → | IND-CCA2 |
| ↓ | ↓ | ↓ | |||
| CCA2 | OW-CCA2 | → | IND-CCA2 | = | NW-CCA2 |
公開鍵暗号方式は、研究の成果により、現在IND-CCA2を満たせるアルゴリズムが発見されています。
このIND-CCA2は、安全性の指標として、NW-CCA2と同等の安全性があります。
具体的には、最も基本的なRSA暗号(参考文献:A Method for Obtaining Digital Signatures and Public Key Cryptosystem)のアルゴリズムは、OW-CPAしか満たしていませんでしたが、OPEP(Optimal Asymmetric Encryption Padding)と呼ばれる改良を加えたRSA-OAEPのアルゴリズムを用いることでIND-CCA2の要件を満たすことができています(参考文献:暗号アルゴリズム評価報告書 RSA-OAEP)。
公開鍵暗号方式の安全性
公開鍵暗号方式のアルゴリズムは、共通鍵暗号方式と同様に計算量的安全性で保証されています。
この計算量的安全性に関して、公開鍵暗号方式に利用されている計算量の保証に関する指標として、安易に解くことができない数学的な問題を2つ紹介します。
素因数分解問題
素因数分解問題とは、「桁数が大きい合成数の素因数分解を求めよ」という問題です。
現在、素因数分解問題のアルゴリズムは、下記の表のようなものがあります。
| アルゴリズム | 内容 |
|---|---|
| 試行割算法 | 合成数 |
| Fermat法 | 合成数 |
| 2次ふるい法 | 2次合同式 |
| 数体ふるい法 | 2次ふるい法を一般化した方法 |
このうち、上2つの方法については、合成数 ![]() のサイズによって計算量が決まるアルゴリズムとなっています。
のサイズによって計算量が決まるアルゴリズムとなっています。
一方で、2次ふるい法と数体ふるい法については、条件を満たすことにより、最速となるアルゴリズムとなっています。
離散対数問題(DLP: Discrete Logarithm Problem)
離散対数問題とは、「整数 ![]() が存在し、
が存在し、![]() が成立する。この際、
が成立する。この際、 ![]() から
から ![]() を求めよ。」という問題です。
を求めよ。」という問題です。
ちなみに、この問題で利用される整数 ![]() には下記の条件が存在します。
には下記の条件が存在します。
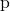 は、1024ビット以上の素数である
は、1024ビット以上の素数である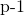 の約数であり、
の約数であり、 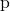 に近いサイズの素数
に近いサイズの素数 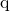 が存在する
が存在する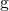 は、
は、 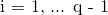 に対して
に対して 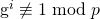 が成立する
が成立する
現在、 ![]() の
の ![]() を求めるアルゴリズムは下記の表のようなものがあります。
を求めるアルゴリズムは下記の表のようなものがあります。
| アルゴリズム | 内容 |
|---|---|
| 列挙法 | |
| Baby-step Giant-step algorithm |
おわりに
今回は、公開鍵暗号方式の安全性に関する知識を紹介しました。ただ、公開鍵暗号方式は利用しやすい暗号方式のため、応用が進んでいる分野です。ブロックチェーンでは、鍵生成に楕円曲線暗号、トランザクションの署名に電子署名の仕組みが利用されており、これらも公開鍵暗号方式の内容のため、今後紹介できればと思います。
参考文献一覧
Author

