暗号技術における安全性(共通鍵暗号方式)
はじめに
ブロックチェーンスタジオでは、個人データの秘匿化に関する研究を行っています。その一環で暗号技術に関する勉強を行っています。今回は、その中で共通鍵暗号方式の安全性に関する基礎的な知識として、下記について紹介したいと思います。
- 共通鍵暗号方式の手法
- 暗号文の秘匿性に関する解説
- 共通鍵暗号方式への攻撃手法
- 暗号技術における安全性の解説
共通鍵暗号方式
概要
共通鍵暗号方式とは、以前の記事で紹介した通り、データの送信者と受信者の間で事前に極秘に鍵を共有し、この鍵を用いてデータの暗号や復号を行いデータの送受信をする方式です。なお、暗号化と復号化を同じ鍵で行う必要があるため、対象鍵暗号方式と呼ばれることもあります。
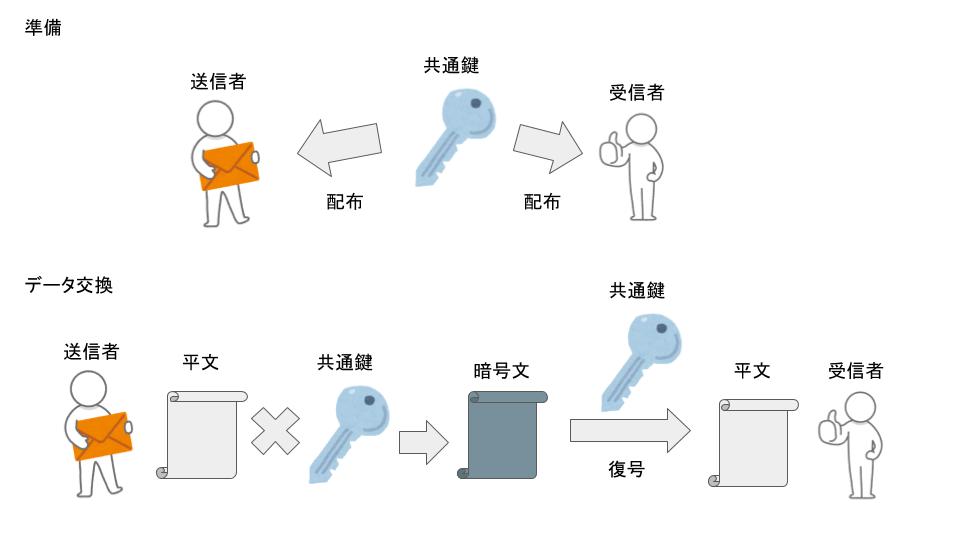
また、上記の図を数式で表すと以下のようになります。共通鍵暗号方式では、下記の数式が成り立つことが前提となっており、これを「正当性を満たす」と定義されています。
平文をm、共通鍵をr、暗号化アルゴリズムをEnc、復号化アルゴリズムをDecと定義する。この時、「m = Dec(r, Enc(r, m))」が成り立つ。
暗号方式の種類
上記の図のように暗号文を生成する際に、一度に平文全てを暗号化する場合、平文が長くなるにつれて共通鍵と暗号文を長くする必要があります。
例) 絶対に破られないことを保証されている共通鍵暗号の1つであるVernam暗号を用いて解説する。
- プロセス
- 準備
平文m(例: 0b1010)と共通鍵r(例: 0b0110)を用意- 暗号アルゴリズム
Enc(m) := m xor r (暗号文e = 0b1100)- 復号アルゴリズム
Dec(e) := e xor r (平文m = 0b1010)- 解説:排他的論理和を取るために平文と同じ長さの共通鍵を用意する必要があり、暗号文も同じ長さになる
このような暗号化方式を実運用しようとすると、想定される平文の長さごとに共通鍵を用意する必要があります。このため、管理する鍵の数が増大し、紛失等のリスクが増大する問題が発生します。そこで、共通鍵の長さを固定化し、平文を区切って暗号化される手法が一般的に利用されています。この手法は、以下の2つに大きく分類されています。
- ブロック暗号:平文を固定長のブロックに分割(長さが足りないブロックはパディングを行う)して暗号化する方式
- ストリーム暗号:平文1ビット(もしくは1バイト)ごとに暗号化する方式
共通鍵暗号方式の解読
暗号技術における秘匿性
攻撃者の解読目標
暗号技術における秘匿性の考え方は、攻撃者の解読目標によって段階的に設定されます。基本的に、攻撃者の解読目標は下記のように段階化されていると定義されています。
- (段階1): 暗号文から平文の部分情報を得ることができる
- (段階2): 暗号文から完全に平文全体を解読できる
- (段階3): 鍵を特定することができる
なお、上記の平文の部分情報というのは、平文の一部の他、暗号文を作成するために利用される関数の値の一部のような情報も含みます。
暗号文のランダム化
攻撃者の解読目標のうち、段階1や段階2を達成する状況というのは、いくつか存在します。例えば、入札用のシステムを考えるとすると、「入札システムとして、商品が落札されると、その際の値段も公表されるようなシステムを考える。この場合、1回目の入札で、A社が10万円で落札したことが公表されると、1回目にA社が登録した暗号文cが10万円だと分かってしまい、2回目以降、同じ暗号文cで入札した人の金額が10万円であることが分かる」という状況があり、この状況は段階2が達成できたと定義されています。
こういった、入力が決まると常に同じ結果を出力するアルゴリズムを「決定的アルゴリズム」と呼びます。一方で、入力が同じでも異なる出力を行うアルゴリズムを「確率的アルゴリズム」と呼びます。
この確率的アルゴリズムでは、暗号文を生成する途中で乱数を用いることが一般的です。例えば、確率的アルゴリズムの1つとしてブロック暗号に用いられるCBC(Cipher Block Chaining)モードと呼ばれる下記の図(wikipediaから引用)のような考え方があります。このCBCモードでは、暗号文を生成する際に、IV(Initialization Vector)と呼ばれる乱数と、分割された平文の最初のブロックを排他的論理和でランダム化した後に暗号化し、残りの平文は、前回暗号化された文字列と排他的論理和を取ってから暗号化するという流れになっています。このため、IVの値によって暗号文が異なり、結果として出力される暗号文の値が異なるようになっています。
このように、確率的アルゴリズムを用いると、攻撃者が暗号文から平文を予測することを困難にすることができるため、秘匿性が高い暗号方式を作成することができます。
共通鍵暗号方式の攻撃手法
攻撃手法の強弱について
暗号技術では、攻撃者が取れる選択肢が多い攻撃手法ほど強力な攻撃手法となっています。また、暗号方式によって、実行できる攻撃手法が異なっています。今回は、共通鍵暗号方式への攻撃手法として定義されているものを5つ紹介したいと思います。なお、上から下にいくにつれて攻撃者の取れる選択肢が多くなっています。
攻撃手法一覧
暗号文単独攻撃(COA: Ciphertext-only attack)
同一の秘密鍵のみを用いて暗号化された暗号文のみを用いて平文を求める攻撃モデルのことを指します。直感的な説明としては、「ある特定の文字を別の文字に変換するだけの暗号(例:シーザー暗号、換字式暗号)を想定する。この場合、英単語はeのような文字が頻繁に利用されるといった特徴があるため、頻出するアルファベットをeと推測し、平文もしくは共通鍵となる変換パターンを解読する」といった攻撃モデルとなります。現在でも、複数の暗号文から、候補となる全ての文字列を鍵として用い、適当な暗号アルゴリズムを当てはめて攻撃するようなこともできるため、現実的ではありませんが、「全ての共通鍵暗号式に対して適用可能な攻撃モデル」と言われています。
既知平文攻撃(KPA: Known Plaintext Attack)
攻撃者が、平文と暗号文の対を偶然手に入れた状況で、解析対象の暗号文から平文や共有鍵を得る攻撃モデルのことを指します。直感的な説明としては、「YesとNoしか平文がないことを想定する。この際、Noを暗号化した暗号文を攻撃者が偶然手に入れた場合、Yesの暗号文を手に入れると、Yesという平文や暗号化に利用する共有鍵を解読できる」という攻撃モデルとなります。
選択平文攻撃(CPA: Chosen Plaintext Attack)
攻撃者が、自由に平文から暗号文を手に入れることができる状況で、解析対象の暗号文から平文や共有鍵を得る攻撃モデルのことを指します。直感的な説明としては、「ある時間に起動すると、その時間(暗号文)に応じてランダムにダンジョンマップ(平文)を生成するゲーム(暗号化オラクル)があると想定する。この状況で、適当に時間を変えて起動したダンジョンマップの傾向を掴み、あるダンジョンマップを生成するための起動時間を導き出す。」という暗号化オラクルを利用した攻撃モデルとなります。
オラクル:要求に応じてデータを返す仮想的な存在のこと。暗号化オラクルは、平文に対して暗号文を返す。
選択暗号文攻撃(CCA, CCA1: Chosen Ciphertext Attack)
解析対象となる暗号文を除き、解析対象となる暗号文を手に入れる前であれば、自由に暗号文から平文を得ることができる(復号化オラクルが存在する)状況で、解析対象となる暗号文の平文や共有鍵を得る攻撃モデルを指します。直感的な説明としては、「ある時間に起動すると、その時間(暗号文)に応じてランダムにダンジョンマップ(平文)を生成するゲームがあり、解析対象となるダンジョンマップを除いてダンジョンマップが表示される時間の解析ずみの対応表(復号化オラクル)が見れる状況を想定し、解析対象となるダンジョンの時間を導き出す。ただし、解析対象が分かった瞬間、対応表は消滅する」という復号化オラクルを利用した攻撃モデルとなります。
適応的選択暗号文攻撃(CCA2: Adaptive Chosen Ciphertext Attack)
解析対象となる暗号文を除き、解析対象となる暗号文を手に入れた後であっても、自由に暗号文から平文を得ることができる(復号化オラクルが存在する)状況で、解析対象となる暗号文の平文や共有鍵を得る攻撃モデルを指します。直感的な説明としては、「ある時間に起動すると、その時間(暗号文)に応じてランダムにダンジョンマップ(平文)を生成するゲームがあり、解析対象となるダンジョンマップを除いてダンジョンマップが表示される時間の解析ずみの対応表(復号化オラクル)が見れる状況を想定し、解析対象となるダンジョンの時間を導き出す。」という復号化オラクルを利用した攻撃モデルとなります。
共通鍵暗号方式の安全性
安全性の指標
暗号方式に対する安全性の指標は、「秘匿性」と「攻撃手法に対する防御手段を持っているか」の組み合わせで決まります。例えば、共通鍵暗号方式の始まりとして有名なDES(Data Encryption Standard)は、決定的アルゴリズムのため、複数の暗号文を手に入れることで、一定の法則性を得ることができるとされています。また、鍵長が56ビットと短いこともあり、計算機技術の発達のため、鍵の組み合わせを網羅できるため暗号文単独攻撃が成立してしまう暗号方式となっています。このため、DESによる暗号方式については、現在使用しないようになり、改良が加えられたTDES(TripleDES)のようなアルゴリズムが発明されています。
なお、計算機技術の発達や、安全とされていたが効率的な解読手法が発見されるといった暗号方式に脆弱性が出てくることを、「暗号の危殆化」と呼びます。
計算量的安全性
共通鍵暗号方式のアルゴリズムは、基本的にブロック暗号方式で開発されています。これは、下記2つの理由があります。
- Vernam暗号の場合、共有鍵を盗まれない限り総当たりで攻撃でしか突破できないが、平文のバイト数ごとに共有鍵を生成する必要があり、実運用に向かない
- ストリーム暗号方式の場合、鍵長の長さが短くなる影響で総当たり攻撃によって破られる計算量が小さくなる
なお、ブロック暗号方式の安全性を測る指標として、計算量的安全性というものが存在します。この計算量的安全性とは、暗号解読に必要な最も効率なアルゴリズムの計算量が現実的に実行不可能であるという指標です。例えば、鍵の長さが ![]() となるブロック暗号のアルゴリズムを用いる場合、総当たり攻撃が最も効率的な攻撃アルゴリズムだと、計算量としては、
となるブロック暗号のアルゴリズムを用いる場合、総当たり攻撃が最も効率的な攻撃アルゴリズムだと、計算量としては、![]() となります。
となります。
おわりに
今回は、共通鍵暗号方式におけるセキュリティに関する基礎的な知識について紹介しました。この考え方については、公開鍵暗号方式を含め、現代暗号の安全性に関する基礎知識となっています。ブロックチェーンでは、トランザクションに残る情報が公開されてしまうので、トランザクションに残す情報を暗号技術を利用して秘匿する必要があります。様々な暗号技術がありますが、サービスとして適用するには、利用する暗号技術に応じて、どういった部分(秘匿性に関する条件、攻撃手法に対する防御手段を持つか否か)に気をつける必要があるのか掘りしないといけないため、暗号技術に関する調査は引き続き行なっていこうと考えています。
参考
Author

